数値計算とか、シミュレーションとか、「なんかすごそう」って思っていませんか?コンピュータって意外と賢くないんです。中で何をしているのか、超簡単に解説します!わかってしまえば、自分でもできそうな気がしてきますよ。
シミュレーションってなに?
シミュレーションって言葉、よく聞きますよね。地球温暖化がどうなっていくのかを予測する、とか、SKラボ.netの中でも、iRICで流況シミュレーションするとか、言っていますが、具体的に何をどうしているのか、簡単に説明しますよ!
世の中のいろいろな現象は「微分方程式」で説明されているんです。シミュレーションって、多くの場合、微分方程式をコンピュータで解いているんです。「ホラ難しい」とか言わないでください。2番目に簡単な微分方程式を使って説明しますね。
二番目に簡単な微分方程式?
一番簡単な微分方程式って、たぶんdy/dx = 定数とか、そんな感じではないでしょうか。でもこれは簡単すぎるし、実用的にも面白くないので、二番目に簡単でも結構実用的な、次の式を見てみましょう。
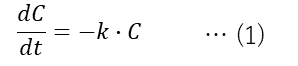
これは、川の中を汚濁物質が流れ下るときの汚濁物質の濃度C [mg/L]の時間変化を表す式です。左辺のdC/dtですが、苦手な方だと1つの記号にしか見えないかもしれませんね。でも、dtは非常に小さい時間、dCはその非常に小さい時間の間のCの変化量を表しています。dCもdtも非常に小さい値ですが、だからといって相互に関係のないとにかく小さな数字というわけではなく、Cとtの変化の比率はどれだけdtとdCが小さくたって維持されているわけです。だからdC/dtはある瞬間のCの変化速度になるわけですね。そしてそれが=-k・Cである、ということですから、(1)式の意味は、Cが大きいほどCは速く減少する、つまり、汚い川の水ほどきれいになる速度が大きい、という式なのですね。kは分解速度係数といいます。
さてこの式は、高校3年だったか大学1年だったかの知識があれば、次のように解くことができます。逆に言えば、そのくらいの知識がないと解けないということでもあります。
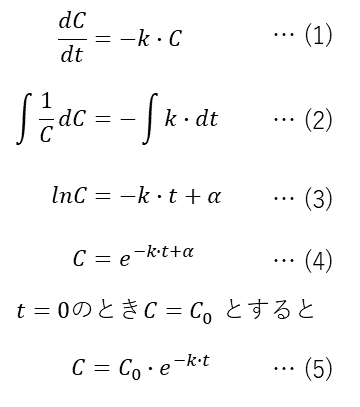
この式のうち、知識が必要なのは、(2)式が(3)式になるところですね。これは暗記していないとわかりません。普通のコンピュータはこれを暗記していないので、この問題を解くことができないのです。(5)式を、微分方程式(1)の解析解といいます。またC0は初期値といいます。
微分方程式をコンピュータにもわかるように書き直す
そこで、微分方程式を次のように書き換えます。

dtは「無限に小さいtの変化」ですが、Δtは「有限に小さいtの変化」です。分子は、時刻tの濃度がCt、そのΔt後の濃度がCt+ΔtですからΔtの時間変化の間の濃度の変化になります。なので、Δtが無限に小さいとき、(6)式は(1)式と同じ意味になります。しかしΔtは無限に小さな値(つまり数字で表現できない値)ではなく、とにかく数字で表すことのできる値ですから、(6)式は(1)式とぴったり同じではなく、(1)式を近似した式ということになります。(1)式を微分方程式というのに対して、(6)式は差分方程式といいます。
(6)式を整理すると(7)式になります。(7)式の右辺にはCt+Δtは含まれていませんので、Ctがわかっていれば四則演算だけでCt+Δtが計算できます。つまり、(2)式から(3)式を導いた知識がなくても、Δtごとの飛び飛びの値ではありますが、(1)式に近い値が計算できます。つまりコンピュータでも微分方程式の近似解が計算できるということです。(7)式から計算されたCの離散的な値の組を数値解といいます。
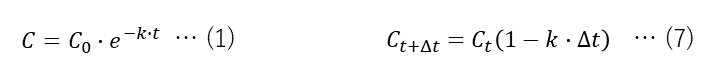
解析解と数値解を比べてみる
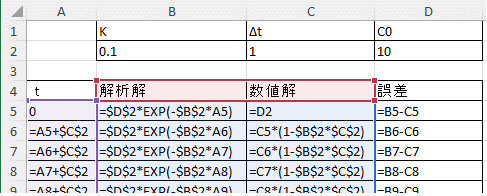
では、解析解と数値解をExcelで比べてみましょう。以下のような式を入れてみます。解析解はどのようなtに対しても値が計算できるのに対して、数値解はΔtごとの値しか得られません。この表では比較するために解析解もΔtごとの値を計算させています。
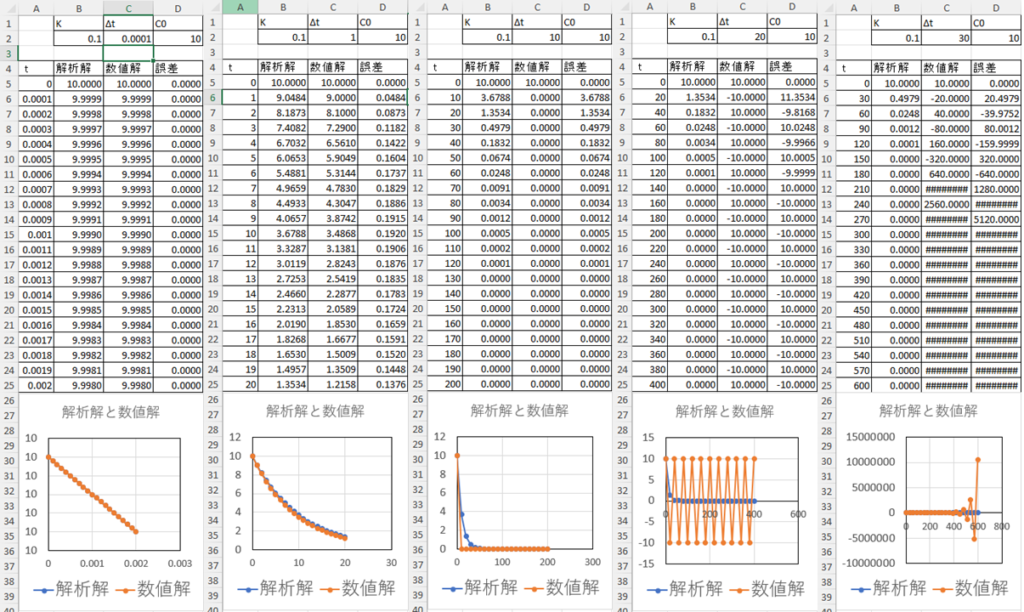
いろいろなΔtに対して同じ計算をしてみたのが下図です。これは、いってみれば、汚濁物質の濃度変化シミュレーションです。濃度10の汚濁水を水路に流したら、t時間流れた時濃度がどうなっているかをシミュレーションしたものですね。
Δtが0.0001の時、誤差は非常に小さく、解析解と数値解が一致しています。Δtが1の時、誤差はありますが、グラフを見るとだいたい同じ結果になっています。Δtが10になると違いが目立ち、Δtが20や30ではまったく違う結果(20は振動している、30は発散しているといいます)になっていることがわかります。
また、同じExcelの行数を費やして計算できた最後のtの値が全然違うこともわかります。Δt=1の時t=20まで結果が得られているのに対し、Δt=0.0001の時、t=0.002までしか結果が得られていません。Δt=0.0001でt=20まで計算しようとすると、Excelの行数は10000倍必要になります。つまり、計算に必要なリソース(時間とかCPUパワーとか)が大変になるということです。
Δtをどのぐらいにすれば良いのかは、わかっていないことが多いです。とりあえず0.1とか1とか10とか2,3の値で計算してみて、結果があまり変わらなければ大きい方の値で良いし、結果が変わるようならより小さな値で試す、といった方法で試行錯誤することになります。
以上から、次のことがわかります。
- 解析解は連続的(どんなtに対しても計算できる)だが、数値解は離散的(Δtごとのとびとびの値)である。
- 数値解には誤差が含まれ、Δtが大きくなると誤差がどんどん大きくなる
- Δtが小さいと誤差も小さいが、計算が大変になる
ですので、誤差を容認できる数値解が得られる範囲でできるだけ大きなΔtを見つけることや、大きなΔtでも誤差が小さくなる差分近似式を見つけることが古来より議論されてきたのです。ちなみに、ここで紹介した差分近似の方法はオイラー法という最も古典的なもので、誤差が大きいために実用的な数値計算で使われることは滅多にありません。
シミュレーションに必要ないろいろの条件について
ここまでのシミュレーションでは、「川を汚濁物質が流れ下る」というイメージでお話ししてきましたが、実際には流れ下る距離などの具体的な場所的広がりは扱っていません。時間軸に沿った変化を扱ってきただけでした。一方、iRICによる流れのシミュレーションなど、実際に場所的な広がりのあるシミュレーションでは、ここまでに出てこなかった計算格子と境界条件も考えなくてはなりません。
場所的な広がりのある物事を表す微分方程式には、dC/dtだけではなく、dC/dxとかdC/dyとか、分母側に位置を表す変数がある項が含まれています。時間がΔtごとの離散的な値だったのと同様、場所についても離散的な飛び飛びの位置について計算されます。その位置を示すのが計算格子です。また、計算する範囲とその外側の”境界”はどう扱うのか、ということを決めなければなりません。これが境界条件です。
本稿の例では初期値を扱いましたが、初期値は、時間経過を計算するとき、未来は永劫に続くとしても、計算を始める最初の時刻というものはどうしても考えないといけないので、過去方向の”境界”としての初期値(初期条件ともいいます)と考えることができます。だとすれば、初期条件は時間軸についての境界条件だといってもよいかもしれません。”とりあえず水を流してみよう“の稿では、三角形の計算格子を生成し、境界条件として、上流側の流量と、下流側の水位を明示的に与えました。河岸となる側面の境界条件は明示的には定義していませんが、どんな水位になっても境界から水が流れ出ないという条件がソルバーのプログラム内で定義されています。
最後にもう一つ、どうなったら計算を止めるのか、という停止条件(終了条件)を決めなければなりません。(未来方向の時間の”境界”条件みたいなものですね。)ある時間まで計算できたら止めるとか、値の変化がある一定量より小さくなったら止めるとか、いろいろな与え方があります。
以上より、シミュレーションをする上でプログラムに与えなければならない要素をまとめると、だいたい以下のようになります。
- Δt(本稿では0.0001から30まで変化させましたね。時間ステップとか計算ステップとかdtとかtime stepとかtime intervalとか、いろいろな呼び名があります。)
- 計算格子(本稿では空間的な広がりを計算しなかったため不要でした。)
- 停止条件(終了条件。本稿の例だとExcelの25行までとか、20回繰り返しとかです。)
- 初期条件(初期値。本稿ではC0=10)
- 境界条件(本稿では空間的な広がりを計算しなかったため不要でした。)
- 微分方程式の中で使われているパラメータの値(本稿ではk=0.1)
SKラボ.netでもiRICなどのシミュレーションを扱っていますが、iRICのソルバーにもたくさんの値を与えないといけません。今与えている値が、上記のいったい何にあたっているのかがわかっていると、それらの値の意味や、計算に与える影響や、どんな値を設定すべきなのかが、なんとなくわかってくるのではないでしょうか。わかってくると楽しくないですか?
Have fun!



コメント