scikit-learnでマシンラーニング入門

Colab

2022.04.26

機械学習フレームワークの定番、scikit-learnのColaboratory上での実行事例集です。できるだけ単純な動作する事例を示します。

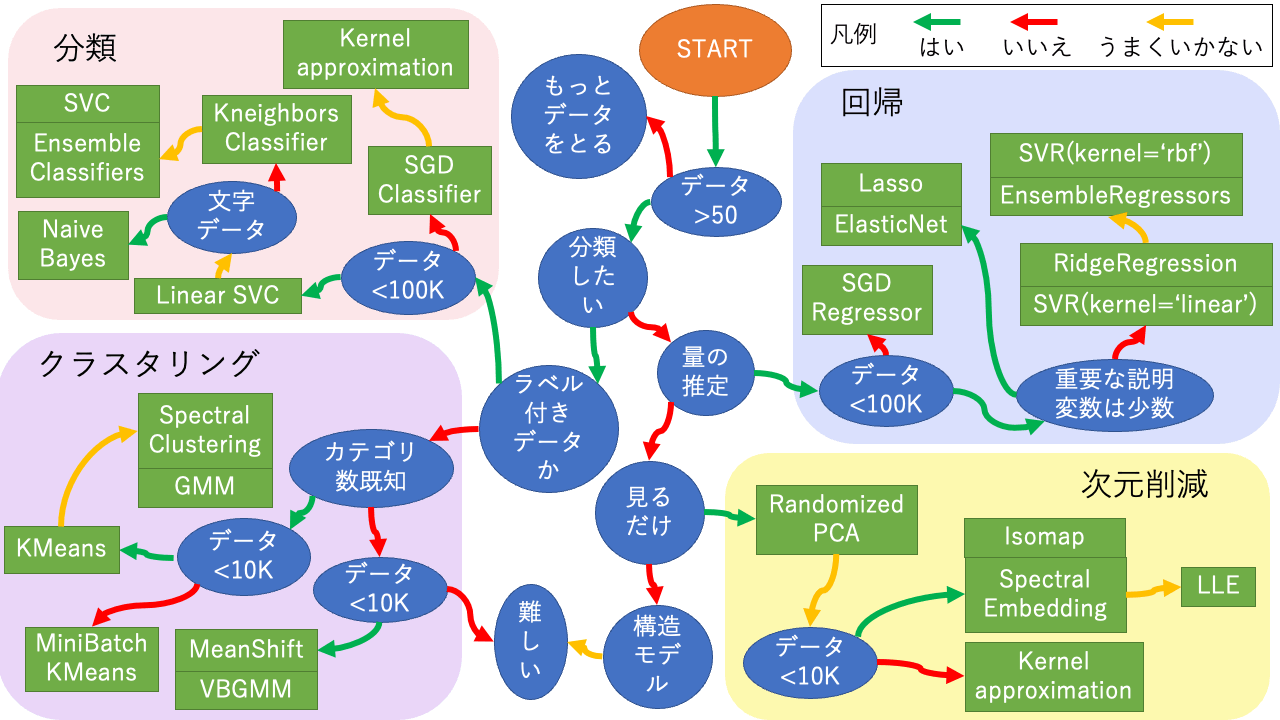
アルゴリズム早見表

scikit-learnの説明の多くはブラウザの翻訳機能でほぼ読める日本語になりますが、この便利な早見表のオリジナルは画像なので機械翻訳されません。元図があまりにも便利なので日本語に書き直してみました。参考になれば幸いです。

図中のアルゴリズムをクリックすると事例にジャンプします。事例はできるだけ簡潔な動作するコードを提示することを目指していますので、実用するにはオリジナルサイトでパラメータ設定等を調べる必要があります。Have fun!

回帰

SGD Regressor

x + y = z を想定したデータ４例で回帰させる例です。データ数が少ないので、コードの例としてみてください。

from sklearn.linear_model import SGDRegressor 
explanatory_variable = [[0,0],[1,0],[0,1],[1,1]]
objective_variable = [0,1,1,2]
reg = SGDRegressor(max_iter=2000, tol=1e-5)
reg.fit(explanatory_variable, objective_variable)
test_data = explanatory_variable
answer = reg.predict(test_data)
print("Input:", test_data,"Output:", answer)

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0.18825169 1.02957579 1.02951829 1.87084239]

オリジナルサイトへ　早見表へ

Lasso

x + y = z を想定したデータ４例で回帰させる例です。データ数が少ないので、コードの例としてみてください。

from sklearn import linear_model
explanatory_variable = [[0,0],[1,0],[0,1],[1,1]]
objective_variable = [0,1,1,2]
reg = linear_model.Lasso(alpha=0.001)
reg.fit(explanatory_variable,objective_variable)
test_data = explanatory_variable
answer = reg.predict(test_data)
print("Input:", test_data,"Output:", answer)

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0.004 1.    1.    1.996]

この例ではalpheがゼロに近いほど正解に近くなります。

オリジナルサイトへ　早見表へ

ElasticNet

x + y = z を想定したデータ４例で回帰させる例です。データ数が少ないので、コードの例としてみてください。

from sklearn import linear_model
explanatory_variable = [[0,0],[1,0],[0,1],[1,1]]
objective_variable = [0,1,1,2]
reg = linear_model.ElasticNet(alpha=0.001)
reg.fit(explanatory_variable,objective_variable)
test_data = explanatory_variable
answer = reg.predict(test_data)
print("Input:", test_data,"Output:", answer)

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0.00399202 1.         1.         1.99600798]

オリジナルサイトへ　早見表へ

RidgeRegression

x + y = z を想定したデータ４例で回帰させる例です。データ数が少ないので、コードの例としてみてください

from sklearn import linear_model
explanatory_variable = [[0,0],[1,0],[0,1],[1,1]]
objective_variable = [0,1,1,2]
reg = linear_model.Ridge(alpha=0.001)
reg.fit(explanatory_variable,objective_variable)
test_data = explanatory_variable
answer = reg.predict(test_data)
print("Input:", test_data,"Output:", answer)

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [9.99000999e-04 1.00000000e+00 1.00000000e+00 1.99900100e+00]

オリジナルサイトへ　早見表へ

SVR(kenrel=’linear’)

SMV（サポートベクタマシン）の回帰問題への拡張です。

x + y = z を想定したデータ４例で回帰させる例です。データ数が少ないので、コードの例としてみてください

from sklearn import svm
explanatory_variable = [[0,0],[1,0],[0,1],[1,1]]
objective_variable = [0,1,1,2]
reg = svm.SVR(kernel='linear')
reg.fit(explanatory_variable,objective_variable)
test_data = explanatory_variable
answer = reg.predict(test_data)
print("Input:", test_data,"Output:", answer)

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0.1 1.  1.  1.9]

オリジナルサイトへ　早見表へ

SVR(kernel=’rbf’)

SMV（サポートベクタマシン）の回帰問題への拡張です。kernelの指定がない場合にはこれが選択されます。

x + y = z を想定したデータ４例で回帰させる例です。データ数が少ないので、コードの例としてみてください

from sklearn import svm
explanatory_variable = [[0,0],[1,0],[0,1],[1,1]]
objective_variable = [0,1,1,2]
reg = svm.SVR(kernel='rbf')
reg.fit(explanatory_variable,objective_variable)
test_data = explanatory_variable
answer = reg.predict(test_data)
print("Input:", test_data,"Output:", answer)

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0.1 1.  1.  1.9]

オリジナルサイトへ　早見表へ

EnsembleRegressors

一般性・ロバスト性を向上させるため、複数の推定器の結果を組み合わせて単一の推定量を得る方法です。ランダムフォレストや袋詰め法など、複数の推定器を独立に構築する平均化法と、AdaBoost, GradientBoostingなど、推定器を順番に構築するブースティング法があります。

事例はすべてx + y = z を想定したデータ４例で回帰させています。データ数が少ないので、コードの例としてみてください

BaggingRegressor

from sklearn.ensemble import BaggingRegressor 
explanatory_variable = [[0,0],[1,0],[0,1],[1,1]]
objective_variable = [0,1,1,2]
reg = BaggingRegressor(n_estimators=100)
reg.fit(explanatory_variable,objective_variable)
test_data = explanatory_variable
answer = reg.predict(test_data)
print("Input:", test_data,"Output:", answer)

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0.31 1.03 0.95 1.67]

RandamForestRegressor

from sklearn.ensemble import RandomForestRegressor 
explanatory_variable = [[0,0],[1,0],[0,1],[1,1]]
objective_variable = [0,1,1,2]
reg = RandomForestRegressor(n_estimators=100)
reg.fit(explanatory_variable,objective_variable)
test_data = explanatory_variable
answer = reg.predict(test_data)
print("Input:", test_data,"Output:", answer)

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0.3  1.04 0.99 1.73]

ExtraTreesRegressor

from sklearn.ensemble import ExtraTreesRegressor 
explanatory_variable = [[0,0],[1,0],[0,1],[1,1]]
objective_variable = [0,1,1,2]
reg = ExtraTreesRegressor(n_estimators=100)
reg.fit(explanatory_variable,objective_variable)
test_data = explanatory_variable
answer = reg.predict(test_data)
print("Input:", test_data,"Output:", answer)

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0. 1. 1. 2.]

AdaBoostRegressor

from sklearn.ensemble import AdaBoostRegressor 
explanatory_variable = [[0,0],[1,0],[0,1],[1,1]]
objective_variable = [0,1,1,2]
reg = AdaBoostRegressor(n_estimators=100)
reg.fit(explanatory_variable,objective_variable)
test_data = explanatory_variable
answer = reg.predict(test_data)
print("Input:", test_data,"Output:", answer)

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [1. 1. 1. 2.]

GradientBoostingRegressor

warm_start可能という特徴があります。

from sklearn.ensemble import GradientBoostingRegressor 
explanatory_variable = [[0,0],[1,0],[0,1],[1,1]]
objective_variable = [0,1,1,2]
reg = GradientBoostingRegressor(n_estimators=100)
reg.fit(explanatory_variable,objective_variable)
test_data = explanatory_variable
answer = reg.predict(test_data)
print("Input:", test_data,"Output:", answer)

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [2.65613989e-05 1.00000000e+00 1.00000000e+00 1.99997344e+00]

　オリジナルサイトへ　早見表へ

分類

SGD Classifier

AND演算（論理積）を学習させる例です。数値データですが演算結果は数字で表されたラベルだと考えると分類問題です。４例ですべての条件を網羅できるのでそもそも機械学習するような問題ではありませんが、コードの例としてみてください。

from sklearn.linear_model import SGDClassifier
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,0,0,1]
clf = SGDClassifier()
clf.fit(learn_data,learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,0,0,1],test_label))

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 0 0 1]
Accuracy score: 1.0

オリジナルサイトへ　早見表へ

kernel approximation

線形アルゴリズムのSGD ClassifierではうまくいかないXOR演算（排他的論理和）を、kernel approximationで変数を高次元化して学習させる例です。

approximation手法は複数あるので、オリジナルサイトを確認してください。

from sklearn.kernel_approximation import RBFSampler
from sklearn.linear_model import SGDClassifier
X = [[0,0],[1,0],[0,1],[1,1]]
y = [0,1,1,0]
rbf_feature = RBFSampler(gamma=1, random_state=1)
X_features = rbf_feature.fit_transform(X)
#print(learn_data_features)
clf = SGDClassifier(max_iter=20)
clf.fit(X_features, y)
print(clf.score(X_features, y))
test_label=clf.predict(X_features)
print(test_label)

実行結果

1.0
[0 1 1 0]

オリジナルサイトへ　早見表へ

Linear SVC

AND演算（論理積）を学習させる例です。数値データですが演算結果は数字で表されたラベルだと考えると分類問題です。４例ですべての条件を網羅できるのでそもそも機械学習するような問題ではありませんが、コードの例としてみてください。

from sklearn.svm import LinearSVC
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,0,0,1]
clf = LinearSVC()
clf.fit(learn_data,learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,0,0,1],test_label))

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 0 0 1]
Accuracy score: 1.0

オリジナルサイトへ　早見表へ

KNeighbors Classifier

XOR演算（排他的論理和）を学習させる例です。数値データですが演算結果は数字で表されたラベルだと考えると分類問題です。４例ですべての条件を網羅できるのでそもそも機械学習するような問題ではありませんが、コードの例としてみてください。

Linear SVCでもできるはずですが、やってみると正解率が悪いために早見表に従ってこの方法をやってみました。

from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,1,1,0]
clf = KNeighborsClassifier(n_neighbors = 1)
clf.fit(learn_data,learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,1,1,0],test_label))

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 1 1 0]
Accuracy score: 1.0

オリジナルサイトへ　早見表へ

SVC

AND演算（論理積）を学習させる例です。数値データですが演算結果は数字で表されたラベルだと考えると分類問題です。４例ですべての条件を網羅できるのでそもそも機械学習するような問題ではありませんが、コードの例としてみてください。

from sklearn.svm import SVC
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,0,0,1]
clf = SVC()
clf.fit(learn_data,learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,0,0,1],test_label))

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 0 0 1]
Accuracy score: 1.0

オリジナルサイトへ　早見表へ

Ensemble Classifiers

一般性・ロバスト性を向上させるため、複数の推定器の結果を組み合わせて単一の推定量を得る方法です。ランダムフォレストや袋詰め法など、複数の推定器を独立に構築する平均化法と、AdaBoost, GradientBoostingなど、推定器を順番に構築するブースティング法があります。

AND演算（論理積）を学習させる例です。数値データですが演算結果は数字で表されたラベルだと考えると分類問題です。４例ですべての条件を網羅できるのでそもそも機械学習するような問題ではありませんが、コードの例としてみてください。

BaggingClassifier

from sklearn.ensemble import BaggingClassifier
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,0,0,1]
clf = BaggingClassifier()
clf.fit(learn_data,learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,0,0,1],test_label))

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 0 0 1]
Accuracy score: 1.0

RandomForestClassifier

from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,0,0,1]
clf = RandomForestClassifier()
clf.fit(learn_data,learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,0,0,1],test_label))

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 0 0 1]
Accuracy score: 1.0

ExtraTreesClassifier

from sklearn.ensemble import ExtraTreesClassifier
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,0,0,1]
clf = ExtraTreesClassifier()
clf.fit(learn_data,learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,0,0,1],test_label))

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 0 0 1]
Accuracy score: 1.0

AdaBoostClassifier

from sklearn.ensemble import AdaBoostClassifier
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,0,0,1]
clf = AdaBoostClassifier()
clf.fit(learn_data,learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,0,0,1],test_label))

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 0 0 1]
Accuracy score: 1.0

GradientBoostingClassifier

from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,0,0,1]
clf = GradientBoostingClassifier()
clf.fit(learn_data,learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,0,0,1],test_label))

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 0 0 1]
Accuracy score: 1.0

HistGradientBoostingClassifier

近年実装されたアルゴリズムで、欠損値をサポートしています。

from sklearn.ensemble import HistGradientBoostingClassifier
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,0,0,1]
clf = HistGradientBoostingClassifier(max_iter=1).fit(learn_data, learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,0,0,1],test_label))

実行結果：この例では正解にたどり着いていません。データまたはパラメータの検討が必要です。

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 0 0 0]
Accuracy score: 0.75

オリジナルサイトへ　早見表へ

Naive Bayes

Gaussian Naive Bayes

from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,0,0,1]
clf = GaussianNB()
clf.fit(learn_data,learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,0,0,1],test_label))

実行結果

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 0 0 1]
Accuracy score: 1.0

Multinominal Naive Bayes

テキスト分類で使用される古典的手法の１つです。

from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,0,0,1]
clf = MultinomialNB()
clf.fit(learn_data,learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,0,0,1],test_label))

実行結果：この例では正解が得られていません。データまたはパラメータの検討が必要です。

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 0 0 0]
Accuracy score: 0.75

Complement Naive Bays

不均衡なデータセットに適しています。

from sklearn.naive_bayes import ComplementNB
from sklearn.metrics import accuracy_score
learn_data = [[0,0],[1,0],[0,1],[1,1]]
learn_label = [0,0,0,1]
clf = ComplementNB()
clf.fit(learn_data,learn_label)
test_data=[[0,0],[1,0],[0,1],[1,1]]
test_label=clf.predict(test_data)
print("Input:", test_data,"Output:", test_label)
print("Accuracy score:", accuracy_score([0,0,0,1],test_label))

実行結果：この例では正解が得られていません。データまたはパラメータの検討が必要です。

Input: [[0, 0], [1, 0], [0, 1], [1, 1]] Output: [0 0 0 0]
Accuracy score: 0.75

オリジナルサイトへ　早見表へ

次元削減

Randomized PCA

いわゆる主成分分析です。例では線形な変動を配列の第一要素ですべて説明できるデータを使っています。

ffrom sklearn.decomposition import PCA
X = [[-3, -1], [-2, -1], [-1, -1], [1, -1], [2, -1], [3, -1]]
pca = PCA(svd_solver='randomized')
pca.fit(X)
print("Components", pca.components_)
print("Explained variance ratio", pca.explained_variance_ratio_)
print("Singular values", pca.singular_values_)

実行結果

Components [[-1. -0.]
 [ 0.  1.]]
Explained variance ratio [1. 0.]
Singular values [5.29150262 0.        ]

オリジナルサイトへ　早見表へ

Isomap

例では線形な変動を配列の第一要素ですべて説明できるデータを使っています。

from sklearn.manifold import Isomap
X = [[-3, -1], [-2, -1], [-1, -1], [1, -1], [2, -1], [3, -1]]
embedding = Isomap()
X_transformed = embedding.fit_transform(X)
print(X_transformed)

実行結果

[[ 3.  0.]
 [ 2.  0.]
 [ 1.  0.]
 [-1.  0.]
 [-2. -0.]
 [-3.  0.]]

オリジナルサイトへ　早見表へ

Spectral Embedding

非線形次元削減です。例では線形な変動を配列の第一要素ですべて説明できるデータを使っています。

from sklearn.manifold import SpectralEmbedding
X = [[-3, -1], [-2, -1], [-1, -1], [1, -1], [2, -1], [3, -1]]
embedding = SpectralEmbedding()
X_transformed = embedding.fit_transform(X)
print(X_transformed)

実行結果：動作はしましたがこのデータではワーニングが出ており良い結果は得られていません。データまたはパラメータの検討が必要です。

[[ 3.92519440e-01 -5.25550374e-01]
 [ 3.87225617e-01  2.05819446e-01]
 [-1.73867544e-01 -3.15275313e-01]
 [ 3.78094095e-01 -1.53625934e-01]
 [ 7.01839331e-01 -7.27743335e-05]
 [ 1.73842736e-01  7.47285557e-01]]
/usr/local/lib/python3.7/dist-packages/sklearn/manifold/_spectral_embedding.py:261: UserWarning: Graph is not fully connected, spectral embedding may not work as expected.
  "Graph is not fully connected, spectral embedding may not work as expected."

オリジナルサイトへ　早見表へ

LLE (Locally Linear Embedding)

非線形次元削減を局所的な主成分分析で解くものです。例では線形な変動を配列の第一要素ですべて説明できるデータを使っています。

from sklearn.manifold import locally_linear_embedding
X = [[-3, -1], [-2, -1], [-1, -1], [1, -1], [2, -1], [3, -1]]
X_transformed, err = locally_linear_embedding(X, n_neighbors=3, n_components=2)
print(X_transformed, "err:", err)

実行結果：動作はしていますがこのデータには適していないようです。データまたはパラメータの検討が必要です。

[[-0.56650584  0.39086062]
 [-0.3783892   0.17256559]
 [-0.18945383 -0.56342621]
 [ 0.18945383 -0.56342621]
 [ 0.3783892   0.17256559]
 [ 0.56650584  0.39086062]] err: 0.6292646829064793

オリジナルサイトへ　早見表へ

kernel approximation

入力の次元を上げた写像を入力とすることで線形アルゴリズムの精度を上げる手法です。オリジナルサイトを調べてください。

オリジナルサイトへ　早見表へ

クラスタリング

MeanShift

[1,1]付近に分布するクラスタと[2,2]付近に分離するクラスタができるようなデータ例です。

from sklearn.cluster import MeanShift
data = [[1,1],[1,0.9],[0.9,1],[2,2],[1.9,2],[2,1.9]]
cls = MeanShift(bandwidth = 0.5)
cls.fit(data)
labels = cls.labels_
cluster_centers = cls.cluster_centers_
print(labels)
print(cluster_centers)

実行結果

[1 1 1 0 0 0]
[[1.96666667 1.96666667]
 [0.96666667 0.96666667]]

オリジナルサイトへ　早見表へ

VBGMM (Variational Bayesian Gaussian Mixture)

[1,1]付近に分布するクラスタと[2,2]付近に分離するクラスタができるようなデータ例です。

from sklearn.mixture import BayesianGaussianMixture
data = [[1,1],[1,0.9],[0.9,1],[2,2],[1.9,2],[2,1.9]]
cls = BayesianGaussianMixture(n_components=2, covariance_type='spherical').fit(data)
print(cls.means_)
print(cls.predict(data))

実行結果

[[1.8411254  1.8411254 ]
 [1.09201331 1.09201331]]
[1 1 1 0 0 0]

オリジナルサイトへ　早見表へ

MiniBatch KMeans

[1,1]付近に分布するクラスタと[2,2]付近に分離するクラスタができるようなデータ例です。

from sklearn.cluster import MiniBatchKMeans
data = [[1,1],[1,0.9],[0.9,1],[2,2],[1.9,2],[2,1.9]]
pred = MiniBatchKMeans(n_clusters=2).fit_predict(data)
print(pred)

実行結果

[0 0 0 1 1 1]

オリジナルサイトへ　早見表へ

KMeans

[1,1]付近に分布するクラスタと[2,2]付近に分離するクラスタができるようなデータ例です。

from sklearn.cluster import KMeans
data = [[1,1],[1,0.9],[0.9,1],[2,2],[1.9,2],[2,1.9]]
pred = KMeans(n_clusters=2).fit_predict(data)
print(pred)

実行結果

[0 0 0 1 1 1]

オリジナルサイトへ　早見表へ

Spectral Clustering

1,1]付近に分布するクラスタと[2,2]付近に分離するクラスタができるようなデータ例です。

from sklearn.cluster import SpectralClustering
data = [[1,1],[1,0.9],[0.9,1],[2,2],[1.9,2],[2,1.9]]
cls = SpectralClustering(n_clusters=2)
cls.fit(data)
labels = cls.labels_
print(labels)

実行結果

[1 1 1 0 0 0]

オリジナルサイトへ　早見表へ

GMM (Gaussian Mixture Model)

[1,1]付近に分布するクラスタと[2,2]付近に分離するクラスタができるようなデータ例です。

from sklearn.mixture import GaussianMixture
data = [[1,1],[1,0.9],[0.9,1],[2,2],[1.9,2],[2,1.9]]
cls = GaussianMixture(n_components=2)
cls.fit(data)
print(cls.means_)
print(cls.predict(data))

実行結果

[[0.96666667 0.96666667]
 [1.96666667 1.96666667]]
[0 0 0 1 1 1]

オリジナルサイトへ　早見表へ

コメント

タイトルとURLをコピーしました